Impulse Function, Signal Classes and Fourier Properties
Posted by Anonymous and classified in Design and Engineering
Written on in  English with a size of 23.38 KB
English with a size of 23.38 KB
Properties of the Impulse Function
Answer
The impulse function, often denoted as the Dirac delta function δ(t), has several important properties that make it a useful tool in mathematics, physics, and engineering, particularly in signal processing and systems analysis. Here are the key properties:
Sifting Property
The most important property of the Dirac delta function is its sifting property. For any continuous function f(t):
∫−∞∞ f(t) δ(t − t0) dt = f(t0)
This means the integral of a function multiplied by the delta function picks out the value of the function at t0.
Normalization
The integral of the delta function over the entire real line equals one:
∫−∞∞ δ(t) dt = 1
Scaling Property
If a is a nonzero constant, then the delta function scales as:
δ(a t) = (1 / |a|) δ(t)
Shifting Property
The delta function can be shifted in time: δ(t − t0) represents an impulse occurring at time t0.
Derivative of the Delta Function
The derivative of the delta function, δʼ(t), satisfies:
∫−∞∞ f(t) δʼ(t − t0) dt = −fʼ(t0)
Convolution with the Delta Function
Convolving a function f(t) with the delta function yields the function itself:
f(t) * δ(t) = f(t)
Classification of Signals
Answer
Signals can be classified based on various criteria including their time domain behavior, amplitude, periodicity, symmetry, energy/power, determinism, and application. Common classifications include:
1. Based on Time Characteristics
- Continuous-time signals: Defined for all time (e.g., analog sine waves).
- Discrete-time signals: Defined only at discrete time instants (e.g., sampled signals).
2. Based on Amplitude Characteristics
- Analog signals: Can take any value in a range (continuous amplitude).
- Digital signals: Take a finite set of values (e.g., binary values 0 and 1).
3. Based on Periodicity
- Periodic signals: Repeat at regular intervals (e.g., sine waves).
- Aperiodic signals: Do not repeat (e.g., noise, transient signals).
4. Based on Symmetry
- Even signals: Symmetric about t = 0 (e.g., cosine).
- Odd signals: Anti-symmetric about t = 0 (e.g., sine).
5. Based on Energy and Power
- Energy signals: Finite energy E = ∫−∞∞ |x(t)|² dt (0 < E < ∞). Examples: pulses, decaying exponentials.
- Power signals: Finite average power but infinite energy. Power P = limT→∞ (1 / 2T) ∫−TT |x(t)|² dt (0 < P < ∞). Examples: sinusoids.
6. Based on Determinism
- Deterministic signals: Exactly described by a mathematical expression (e.g., sinusoids).
- Random signals: Characterized statistically (e.g., noise).
7. Based on Applications
- Communication signals: For information transmission (audio, video).
- Control signals: Used to regulate systems.
- Sensor signals: Generated by sensors (temperature, pressure).
Periodic and Aperiodic Signals
Answer
Periodic and aperiodic signals are key in signal processing and communications:
Periodic Signal
A signal x(t) is periodic if there exists a fundamental period T such that:
x(t) = x(t + T) for all t.
Examples: sine wave, square wave. Characteristics: definite period T, repetitive, representable by Fourier Series.
Aperiodic Signal
An aperiodic signal does not repeat at fixed intervals and has no fundamental period. Examples: exponentially decaying signals, speech, noise. Typically analyzed with the Fourier Transform rather than Fourier Series.
Key difference: Periodic signals exhibit cyclic behavior; aperiodic do not.
Complex Exponential
Answer
A complex exponential has the form:
x(t) = A e^{j(ω t + φ)}
where A is amplitude, j is the imaginary unit, ω is angular frequency, and φ is phase.
Key Properties
- Euler's formula: e^{jθ} = cos(θ) + j sin(θ).
- Oscillatory behavior: Represents sinusoidal oscillations.
- Real and imaginary parts: A e^{jωt} = A cos(ωt) + j A sin(ωt).
- Fourier analysis: Complex exponentials form the basis for Fourier Series and Transforms.
- Multiplicative property: e^{j a} ⋅ e^{j b} = e^{j(a + b)}.
- Period: Repeats every 2π / ω.
Energy and Power Signals
Answer
Signals are classified by their energy and power:
Energy Signal
Signal x(t) is an energy signal if its energy E = ∫−∞∞ |x(t)|² dt is finite (0 < E < ∞). Typical examples: pulses, decaying exponentials.
Power Signal
Signal x(t) is a power signal if it has finite nonzero average power but infinite energy. Power is computed as:
P = limT→∞ (1 / 2T) ∫−TT |x(t)|² dt
Examples: sinusoidal signals, ongoing random processes.
Key differences
Energy: finite vs infinite. Power: zero vs finite. Energy signals are often transients; power signals model persistent oscillatory behavior.
Bounded and Unbounded Signals
Answer
Signals are bounded if their amplitude remains within a finite value M for all time:
|x(t)| ≤ M for all t (M finite).
Unbounded signals grow without bound as t → ∞ (e.g., exponential growth, ramp functions). Bounded signals are preferred in control and engineering to ensure stability.
Discrete-Time Signal and Its Representation
Answer
Discrete-time signals are defined only at discrete instants and are denoted x[n], where n is an integer. Representation methods include:
- Graphical representation
- Functional representation
- Tabular representation
- Sequence representation
Graphical Representation of Discrete-Time Signals
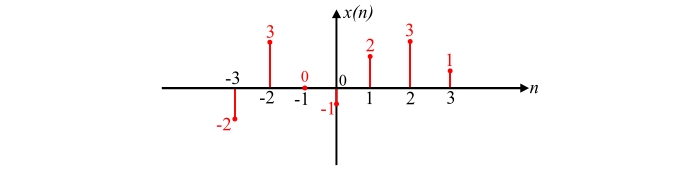
Consider the discrete-time signal x[n] with values:
x[−3] = −2, x[−2] = 3, x[−1] = 0, x[0] = −1, x[1] = 2, x[2] = 3, x[3] = 1
This discrete-time signal can be represented graphically (see figure below):
Functional Representation of Discrete-Time Signal
Writing magnitude against n gives:
x[n] = { −2 for n = −3; 3 for n = −2; 0 for n = −1; −1 for n = 0; 2 for n = 1; 3 for n = 2; 1 for n = 3 }
Tabular Representation of Discrete-Time Signal
Sample index n and the corresponding x[n] value in table form:
| n | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| x[n] | −2 | 3 | 0 | −1 | 2 | 3 | 1 |
Sequence Representation of Discrete-Time Signal
The sequence representation lists the samples; the arrow denotes n = 0:
x[n] = { −2, 3, 0, −1, 2, 3, 1 ↑ }
When no arrow is shown, the first term corresponds to n = 0 by convention.
Sum and Products of Discrete-Time Sequences
Sum: The sum of two sequences is element-wise: if c[n] = a[n] + b[n], then c[n] = a[n] + b[n].
Product: The product of two sequences is element-wise: c[n] = a[n] · b[n].
Scalar multiplication: The product of a sequence and a constant k yields c[n] = k · a[n].
Tabular Representation of Discrete-Time Signal: (duplicate content retained as required)
| n | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| x[n] | −2 | 3 | 0 | −1 | 2 | 3 | 1 |
Operations on Discrete-Time Signals (DTS)
Answer
Operations on discrete-time signals include mathematical manipulations useful for analysis and processing.
1. Basic Operations
- Addition: y[n] = x1[n] + x2[n]
- Subtraction: y[n] = x1[n] − x2[n]
- Multiplication (element-wise): y[n] = x1[n] · x2[n]
2. Time Shifting
- Advance (right shift): y[n] = x[n − k]
- Delay (left shift): y[n] = x[n + k]
3. Scaling
- Amplitude scaling: y[n] = A x[n]
- Time scaling: y[n] = x[k n]
4. Folding (Time Reversal)
Reflect the signal across n = 0: y[n] = x[−n]
5. Convolution
Fundamental operation for linear systems:
y[n] = Σk=−∞∞ x1[k] · x2[n − k]
Used for system analysis, filtering, and digital communications.
6. Differencing (First Difference)
Numerical differentiation: y[n] = x[n] − x[n − 1]
7. Accumulation (Summation)
Discrete integration over time: y[n] = Σk=−∞n x[k]
Relationship Between Impulse and Step Function
Answer
The impulse (delta) and step functions are closely related via differentiation and integration.
1. Impulse Function (Dirac Delta)
- The impulse δ(t) is zero everywhere except at t = 0 and integrates to one: ∫−∞∞ δ(t) dt = 1.
- It models a sudden instantaneous change.
2. Step Function (Unit Step)
The unit step u(t) is defined as:
u(t) = { 1, t ≥ 0; 0, t < 0 }
It represents a signal that switches ON at t = 0.
3. Relationship
Differentiation
The derivative of the unit step yields the delta:
d/dt u(t) = δ(t)
Integration
The integral of the delta yields the unit step:
∫−∞t δ(τ) dτ = u(t)
4. Physical Interpretation
- The impulse models an instantaneous force or change.
- The step models a cumulative effect (switching from OFF to ON).
Properties of the Delta Function (Summary)
Answer
Key properties already noted include:
1. Sifting Property
∫−∞∞ f(t) δ(t − a) dt = f(a)
2. Integral Property
∫−∞∞ δ(t) dt = 1
3. Time Scaling
δ(a t) = (1 / |a|) δ(t)
4. Time Shifting
δ(t − a) represents an impulse at t = a.
5. Differentiation
d/dt u(t) = δ(t)
6. Fourier Transform
The Fourier transform of δ(t) is a constant in frequency (contains all frequencies equally): F{δ(t)} = 1
Static and Dynamic Systems
Answer
Static System
A static (memoryless) system's output depends only on the current input. Characteristics: no memory, instantaneous response. Examples: algebraic relations like V = IR.
Dynamic System
A dynamic system has memory; the output depends on current and past inputs and evolves over time. Often described by differential or difference equations. Examples: circuits with capacitors/inductors, mechanical systems with inertia.
Key Differences
| Property | Static System | Dynamic System |
|---|---|---|
| Memory | No memory | Has memory |
| Response | Instantaneous | Evolves over time |
| Equation Type | Algebraic | Differential or difference |
Causal, Non-Causal and Anti-Causal Systems
Answer
Classification by causality:
- Causal system: Output at time t depends only on present and past inputs. (Real-time physical systems are typically causal.)
- Non-causal system: Output depends on future inputs as well as past/present. Used in offline processing or theoretical analyses.
- Anti-causal system: Output depends only on future inputs (not physically real-time implementable).
Time-Invariant and Time-Variant Systems
Time-invariant systems preserve the shape of responses under time shifts. Time-variant systems have properties that change with time (e.g., varying gain).
| Feature | Time-Invariant | Time-Variant |
|---|---|---|
| Response Shift | Maintains shift | Changes with time |
| Equation Stability | Remains same | Varies over time |
Linear and Nonlinear Systems
Answer
Linear systems obey superposition and scaling. Nonlinear systems do not.
Linear System
- Superposition: x1 → y1 and x2 → y2 implies x1 + x2 → y1 + y2.
- Scaling: k x(t) → k y(t).
- Characteristics: predictable, analyzable by linear methods.
Nonlinear System
- Does not satisfy superposition or scaling. Can exhibit complex behaviors such as chaos and bifurcations.
- Often requires numerical methods for analysis.
Key Differences
| Property | Linear System | Nonlinear System |
|---|---|---|
| Superposition | Holds | Does not hold |
| Scaling | Holds | Does not hold |
| Complexity | Simple | Complex, possibly chaotic |
Stable and Unstable Systems
Answer
System stability describes whether bounded inputs produce bounded outputs (BIBO stability).
Stable System
If |x(t)| is bounded, then |y(t)| is bounded. Stable systems' responses settle and remain predictable.
Unstable System
A bounded input can produce an unbounded output (|y(t)| → ∞). This requires stabilization techniques.
Marginally Stable
System that neither grows unbounded nor decays; it oscillates indefinitely (e.g., ideal undamped LC circuit).
Key Differences
| Property | Stable | Unstable | Marginally Stable |
|---|---|---|---|
| Output Growth | Bounded | Unbounded | Neither decays nor grows |
Invertible and Non-Invertible Systems
Answer
An invertible system allows recovery of the input uniquely from the output; a non-invertible system loses information.
Invertible System
There exists an inverse system H−1 such that H−1[y(t)] = x(t). Example: multiplication by a nonzero constant.
Non-Invertible System
No unique inverse exists; information loss occurs (e.g., squaring function y = x²).
Continuous-Time Fourier Series (CTFS)
Answer
CTFS decomposes a periodic signal into complex exponentials:
x(t) = Σn=−∞∞ Cn e^{j n ω0 t}
where ω0 = 2π / T and the Fourier coefficients are:
Cn = (1 / T) ∫0T x(t) e^{−j n ω0 t} dt
Alternate Sinusoidal Form
x(t) = A0 + Σn=1∞ [An cos(n ω0 t) + Bn sin(n ω0 t)]
Properties and Applications
- Periodicity, orthogonality, convergence conditions.
- Used in signal analysis, audio and image processing, circuit frequency response.
Properties of Fourier Series
Answer
- Linearity: Fourier coefficients add for sum of signals.
- Periodicity: Applies only to periodic signals.
- Symmetry: Even signals contain only cosines; odd signals only sines.
- Time shifting: Shifts introduce phase factors to coefficients.
- Frequency shifting, convolution, differentiation/integration, Parseval's theorem, Gibbs phenomenon.
Properties of Fourier Transform
Answer
The Fourier Transform converts time-domain signals into frequency-domain representations. Key properties include:
- Linearity
- Time shifting: x(t − t0) ⇒ X(f) e^{−j 2π f t0}
- Frequency shifting
- Convolution: Time-domain convolution ⇒ frequency-domain multiplication.
- Differentiation in time ⇔ multiplication by j 2π f in frequency.
- Parseval's theorem: energy equality between time and frequency domains.
- Time scaling and duality.
- Inverse Fourier Transform: x(t) = ∫−∞∞ X(f) e^{j 2π f t} df
Properties of the DTFT
Answer
The Discrete-Time Fourier Transform (DTFT) analyzes discrete signals in frequency domain. Key properties:
- Linearity
- Time shifting: x[n − n0] ⇒ e^{−j ω n0} X(ω)
- Frequency shifting
- Convolution: Time-domain convolution ⇒ frequency-domain multiplication.
- Parseval's theorem: Σn |x[n]|² = (1 / 2π) ∫−ππ |X(ω)|² dω
- Periodicity: DTFT is 2π-periodic: X(ω) = X(ω + 2π).
- Duality: symmetry between time and frequency representations.
Key Causality Differences (Summary Table)
| Type | Depends on Past | Depends on Present | Depends on Future |
|---|---|---|---|
| Causal | Yes | Yes | No |
| Non-Causal | Yes | Yes | Yes |
| Anti-Causal | No | No | Yes |
Causality is a crucial concept in control systems, signal processing, and physics.
