Probability and Set Theory: Key Concepts and Formulas

De Morgan's Law

De Morgan's Law: (Flip if the union is true)

, image of set: [min, max]; one-to-one: horizontal line test; Onto: Image must equal domain; Bijective: one-to-one and Onto

|| EV

||

Possible Outcomes and Probability Calculations

• Repetition formula: n^k
  • Example: 5 awards (k) and 30 students (n), with no limit to awards per student.
• Permutation formula: P(n, k) = n! / (n - k)!
  • Example: Each student gets 1 award, so the number of students decreases by one each award.
• No overlap probability: P(n, k) / repetition formula
• Arrangements: a = slots → a! can be multiplied by arrangements within slots
• Die sum probability:
  • List combinations that lead to the sum for each die.
  • If a die is rolled multiple times, each combination has (rolls)! permutations.
  • Add up the permutations.
  • The sample space in this case is 6ⁿ rolls, so permutations / sample space = Probability.
• Grid problem:
  • List total movements, i.e., ups and rights.
  • The number of paths is equal to total! / (U! * R!).
  • Cross through a point: paths to the point multiplied by paths from the point.
• 
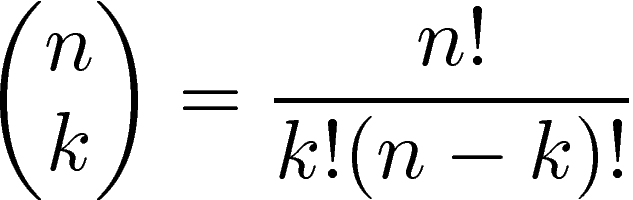
• Students in class probability:
  • Even student distribution g per class → Class A, B, C
  • k students of interest
  • Class population n
  • Probability that all students of interest are in class A: (n - k choose g - k) / (n choose g)
  • Probability that all students of interest are in any class: number of classes * previous probability

Events and Probability

• Events:
  • Example: events E, F, G
  • At least 1 event occurs = E ∪ F ∪ G
  • At least 2 occur = (E ∩ F) ∪ (F ∩ G) ∪ (G ∩ E)
  • None occur = E^c ∩ F^c ∩ G^c
  • At most 2 occur = (E ∩ F ∩ G)^c
• Example: Students in a class, 60% love coffee, 70% love chocolate, 40% love both. What is the probability that a random selection is neither?
• P(A) = 0.6, P(B) = 0.7, P(A ∩ B) = 0.4
• Interest in P(A^c ∩ B^c) can be found using De Morgan's Law = 1 - P(A ∪ B) = 1 - (0.6 + 0.7 - 0.4) = 0.1
• Example: Six-sided loaded die, even face is twice as likely. What is the probability model for 1 roll? Find the probability that the outcome is less than 4.
• Determine probabilities: x = P({1}) = P({3}) = P({5}), y = P({2}) = P({4}) = P({6})
• y = 2x
• Axiom 2/3 → 1 = P{1-6} = 3x + 3y = 9x = 1
• x = 1/9
• y = 2/9
• P(1, 2, 3) = 4/9

Conditional Probability and Bayes' Theorem

• Example: The probability of winning a dice toss is q. A starts, and if he loses, the die is passed to B, who attempts to win. This continues back and forth until one wins. What are the respective probabilities of winning?
• P(A wins) = sum(k = 0, ∞) (1 - q)^2k * q
• Geometric sum:
• P(A wins) = 1 / (2 - q), P(B wins) = 1 - P(A wins) = (1 - q) / (2 - q)
• Communication system: P(good connection) = 0.8; P(bad connection) = 0.2; Error in transmission: P(error | good) = 0.1; P(error | bad) = 0.3; P(good transmission)?
• P(E^c) = P(E^c | G) * P(G) + P(E^c | G^c) * P(G^c) = 0.9 * 0.8 + 0.7 * 0.2 = 0.86

(E ∩ F) ∪ (F ∩ G) ∪ (G ∩ E)